Optimal Covariance Control

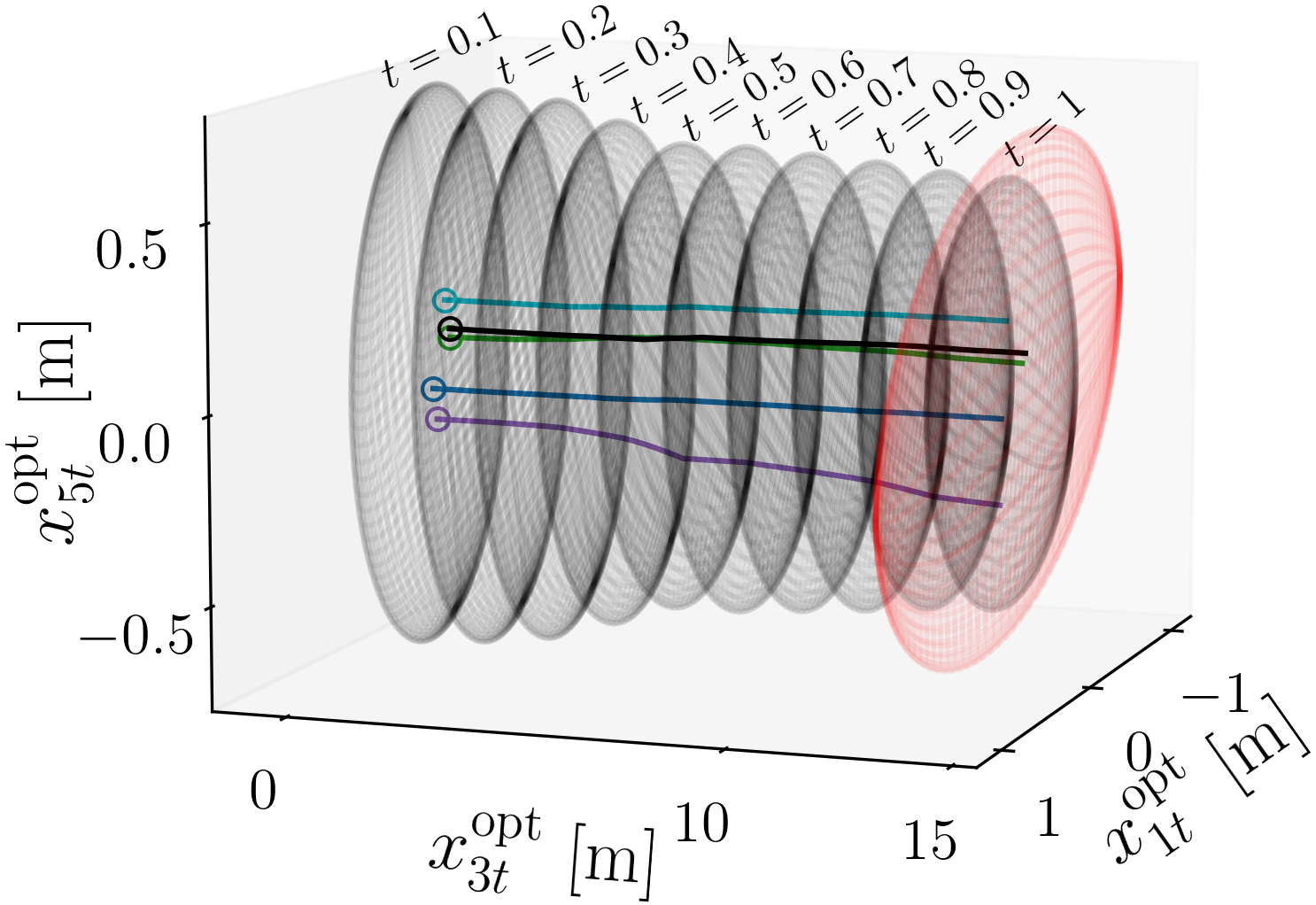
(a) Position covariances

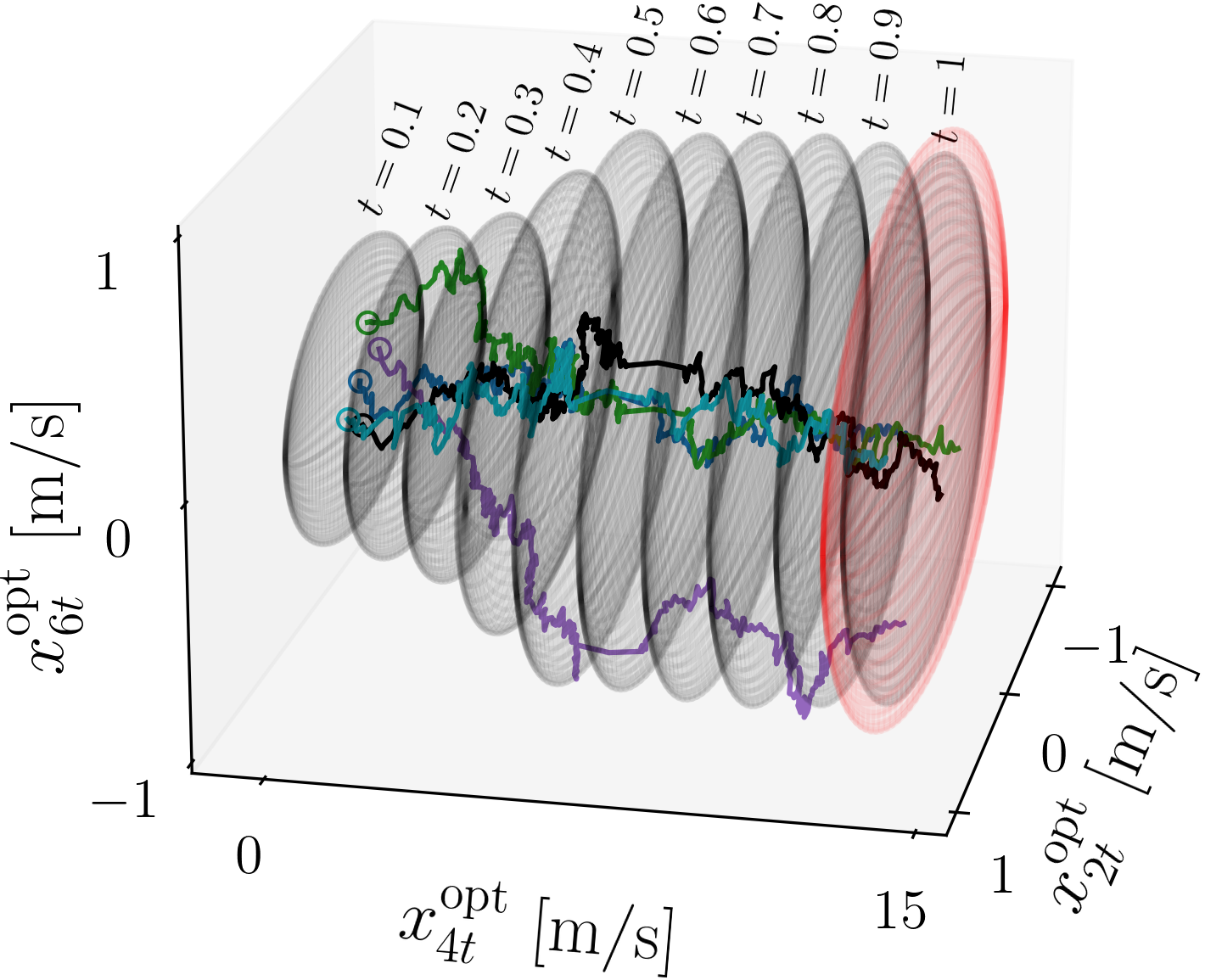
(b) Velocity covariances

Fig. Optimally controlled covariances (gray wireframe ellipsoids) and 5 closed-loop state sample paths for the Noisy CW model in the (a) position and (b) velocity coordinates. The hollow circular markers denote the initial conditions for these sample paths. The red wireframe ellipsoids correspond to the position and velocity marginal covariances of Σ_d.

My Master’s thesis under Professor Abhishek Halder is focused on designing an Optimal Covariance Steering Algorithm in Continuous Time with Hilbert-Schmidt Terminal Cost for Linear Stochastic Systems over a finite time horizon. While there has been a growing literature on the fixed-horizon LQ covariance steering problems with terminal cost for the discrete-time case, its continuous-time version remains relatively unexplored. A key reason behind the imbalance of literature between the discrete-time and continuous-time formulations lies in computational tractability. The discrete-time LQ covariance steering problem with terminal cost naturally leads to a semidefinite program, which is readily solvable using off-the-shelf interior-point solvers. In contrast, the continuous-time formulation with terminal cost gives rise to a coupled nonlinear system of matricial ODEs, for which a principled and computationally efficient algorithm has remained unclear. Building upon this foundation, my current research introduces a soft constraint via the Hilbert–Schmidt Terminal Cost, together with a quadratic cost function for control input and state. For this problem, the necessary conditions of optimality lead to a coupled matrix ODE two-point boundary value problem with nonlinear split boundary conditions. To solve this system of equations, I’ve designed a Matricial Recursive Algorithm with a fast convergence rate. The algorithm and its analysis are grounded in linear fractional transformations parameterized by the state transition matrix of the associated Hamiltonian system. The proposed algorithm was tested and validated on a close-proximity rendezvous scenario by modeling the relative motion of a service spacecraft to a target satellite in LEO using Clohessy–Wiltshire dynamics with stochastic disturbances. Our broader motivation is to ultimately derive a custom algorithm to solve the boundary value problem with a Wasserstein terminal cost. This work takes a significant step in that direction, laying the algorithmic groundwork toward handling the full Wasserstein gradient in future extensions. The code for this project can be found here.

In-Orbit Servicing

Research into the autonomy of spacecraft has been of increasing interest. Indeed, with a growing debris population, robots that can perform routine tasks autonomously (such as simple repairs/maintenance, refueling, or debris removal) may become increasingly essential for actively preventing disaster. In this context, several autonomous missions to uncooperative targets (which generally can be tumbling and orbiting the Earth elliptically) will require rendezvous and docking procedures. In this project, I’ve worked on designing a Control Scheme for a Thrust vectoring Satellite using a Koopman operator-based approach for it to rendezvous with a tumbling noncooperative Satellite under the guidance of Dr. Debasish Ghose, a professor of the Department of Aerospace Engineering at the Indian Institute of Science (IISc), Bengaluru. You can check out my Thesis manuscript and the Codebase for more details.

Earth-Moon Low-Thrust Trajectory Optimization

Fig. Optimal thrust direction and flight path angles: Earth-Escape Phase.

This work was completed as my final project for the course: AERE 6510 - Space Trajectory Optimization under the guidance of Professor Ossama Abdelkhalik. In this project, I extended the classic three-stage method for computing optimal low-thrust trajectories from low Earth orbit (LEO) to low lunar orbit (LLO) originally proposed by Pierson and Kluever (1994). The original three-stage method systematically decomposes the complex optimal trajectory problem into simpler subproblems involving maximum-energy Earth-escape and moon-capture spirals, an all-coasting translunar trajectory, and finally, a complete optimization using a hybrid direct/indirect numerical method. Unlike the original formulation, which assumes a constant thrust magnitude, my work allowed thrust magnitude to be a free variable within the optimal control framework. Starting from the necessary conditions for optimality, I derived the modified equations and solved them numerically to obtain optimal trajectories. The classical restricted three-body problem dynamics govern the spacecraft trajectory, involving highly sensitive numerical computations and optimization strategies. Our extended methodology enables a more flexible and general approach to modeling low-thrust Earth–Moon transfers. Simulation results demonstrated the effectiveness of the approach, yielding energy-efficient transfer trajectories that improve upon the constant-thrust assumption. You can check out the codebase for more details.

Autonomous Mars Rover

In 2020, I co-founded CRISS Robotics, a student research technical team for designing and manufacturing an all-terrain 6-wheeled autonomous Mars rover. I developed the high-level electrical architecture and an electronic differential-based drive control system for the rover there, capable of autonomous traversal, equipment servicing using a 6-DOF robotic manipulator, and life detection using a science module. CRISS qualified for the International Rover Challenge in the 2022 finals at Chennai, India, among 16 international teams, and then won the International Rover Design Challenge in 2023. You can check out the IRC Report and IRDC Report here.

Flight Stabilizing Controllers for Agile Fixed-Wing UAV

In this project, I’ve designed flight stability controllers for an agile fixed-wing UAV under Professor Bijoy Krishna Mukherjee, Department of EEE at BITS Pilani. In particular, I designed and modeled the Longitudinal and Lateral-Directional stability movement controllers of the UAV using the Backstepping Control technique using MATLAB and Simulink. Additionally, I created a wind observer to incorporate environmental disturbances(like wind shears, wind gusts, and atmospheric disturbances) to make the controllers robust and, thus, improve flight capability. The code for this project can be found here.

Powertrain of a Formula-Style Electric Vehicle

Fig. High-level Electrical Architecture of EV

In my freshman year, I joined the Electric Powertrain Subsystem at Inspired Karters Electric, the Formula Student Electric Vehicle (FSEV) Team of BITS Pilani, Pilani Campus. The team comprises roughly 50 talented and focused members who work tirelessly throughout the year to build a single-seater Formula One Car. With endurance being the primary goal of our first electric vehicle, I developed a high-fidelity model of the electric powertrain package by leveraging Simulink & Simscape to calculate the torque and current requirements for motor selection, battery capacity requirements, and optimization of motor control strategies. The powertrain model was incorporated into our proprietary laptime simulator to validate our endurance-optimized design. My brief experience in the Mechanical subsystem also allowed me to assemble and package the electrical components of our car’s CAD model using Fusion 360. Our team achieved an overall first position across India in the 4th Annual Formula Student Electric Vehicle (FSEV) Concept Challenge, hosted by Formula Bharat in the summer of 2020. Subsequently, I gained the opportunity to head the Electric Powertrain Subsystem, as we began manufacturing the EV to showcase in the Formula Bharat competition. You can check out the Design Report and the CAD video here.

Autonomous Delivery Quadcopter

Fig. Flight Control Architecture

In today’s fast-paced world, the integration of Unmanned Aerial Vehicles (UAVs) has marked a paradigm shift in various industries, particularly in transportation and logistics. Among these cutting-edge technologies, autonomous quadcopters have emerged as frontrunners in revolutionizing the delivery landscape. In this project, I’ve designed autonomous navigation (flight attitude, position control, & obstacle avoidance) algorithms using ROS, Python, and Gazebo for a 3-D simulated quadcopter capable of autonomously delivering packages in an urban environment. To detect QR tags on delivery packages, I implemented a pyzbar library-based computer vision algorithm. This project was designed for the e-Yantra Robotics Competition hosted by IIT Bombay and sponsored by the Ministry of Education of India. The code for this project can be found here.